El teorema de Shannon

En 1948 se publicó dentro de la revista de los laboratorios Bell (EEUU) un artículo titulado “A Mathematical Theory of Communication” por el investigador de dicho laboratorio Claude E. Shannon. Dicho artículo, de aproximadamente 50 páginas de extensión, es un complejo análisis matemático donde se establece la velocidad máxima en bits por segundo que se puede alcanzar en cualquier sistema de comunicación real. Claude E. Shannon realizó dicho estudio sobre un sistema de comunicación en general, sin particularizar en ningún medio de transmisión en concreto, por lo que a lo largo de todo el artículo no aparece ninguna mención a componentes o circuitos eléctricos, electrónicos, ópticos o cualquier otro sistema susceptible de emplearse en comunicaciones digitales. Es, como su propio título indica, una teoría matemática de la comunicación. En la siguiente imagen se muestra un fragmento del teorema de Shannon

Como se ha indicado anteriormente, Shannon estudia el caso general de un sistema de comunicación, compuesto por un emisor, un receptor, un canal de transmisión y una fuente de ruido, que en todo sistema real de transmisión existe en mayor o menor medida. En la siguiente imagen se muestra la representación del propio Shannon de dicho sistema general de comunicaciones.

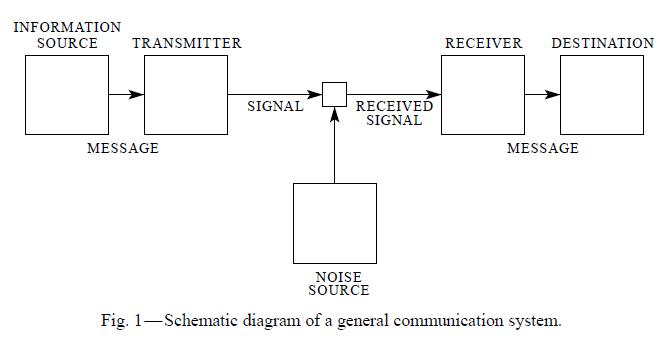A partir del esquema anterior y a lo largo de más de cincuenta páginas, Claude E. Shannon demuestra mediante complejos cálculos matemáticos su famoso teorema de las comunicaciones. Todo el artículo está lleno de límites, derivadas, integrales, cálculos de estadística y probabilidades y otros procedimientos matemáticos.  En la siguiente imagen se muestra un ejemplo de dichos cálculos

Afortunadamente el resultado final del teorema de las comunicaciones de Shannon es una pequeña fórmula, fácil de aplicar y de recordar, y de consecuencias fundamentales para todos los sistemas de comunicaciones modernas: 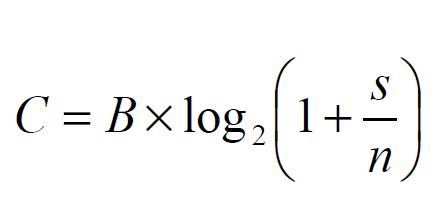En la fórmula de Shannon, C es la velocidad máxima en bits por segundo, B es el ancho de banda en Hz y S/N es la relación señal a ruido (signal/noise), sin unidades. Para cualquier sistema de transmisión con un determinado ancho de banda y con una relación dada de señal a ruido, el teorema de Shannon limita la velocidad máxima en bps que se puede obtener, sea cual sea la técnica de transmisión empleada. El límite de velocidad que impone el teorema de Shannon a cualquier sistema real de transmisión hay que entenderlo de la misma manera que existe una temperatura de cero absoluto y por debajo de la cual no se puede bajar o el límite de la velocidad de la luz, por encima de la cual no se puede subir. Y esto es válido para cualquier sistema de transmisión (fibra óptica, radio, cable de pares, cable coaxial, etc). Ni se puede sobrepasar hoy en día ese límite ni tampoco se podrá sobrepasar en el futuro.

Por ejemplo, en un sistema de comunicaciones como es la telefonía analógica, que utiliza un ancho de banda de 3100 Hz (300-3400) y tiene una relación de señal a ruido de unos 35,5 dB (la señal es aproximadamente 3548 veces mayor que el ruido), la velocidad máxima que se podrá obtener será de:

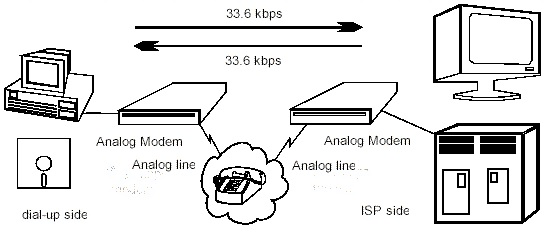
Este valor es el límite teórico impuesto por el Teorema de Shannon, al cual los modems sobre linea analógica se han acercado pero nunca lo han igualado. Por eso estos modems sobre líneas analógicas han tenido como velocidad máxima  33600 bps, y eso a costa de utilizar complejas codificaciones y modulaciones de la señal, que en ausencia de condiciones óptimas de la línea, obliga siempre a los modems a negociar una velocidad aun más baja.

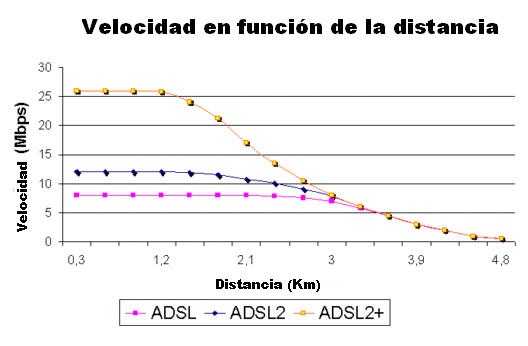
Un caso similar lo tenemos en los accesos ADSL, donde frecuentemente los usuarios demandan velocidades que a determinada distancia de la central no es posible suministrar, se haga lo que se haga. ¿Por qué no es posible dar, por ejemplo, 20 Mbps a un usuario que vive a 5 Km de la central y sin embargo si es posible dar dicha velocidad a uno que vive a 300 metros de la central? La respuesta de nuevo está en el teorema de Shannon: el usuario que vive a 5 km de la central tiene un bucle de abonado o par de hilos de cobre con un ancho de banda muy inferior respecto del que vive a 300 metros de la central y además, también tendrá con seguridad una peor relación señal a ruido.

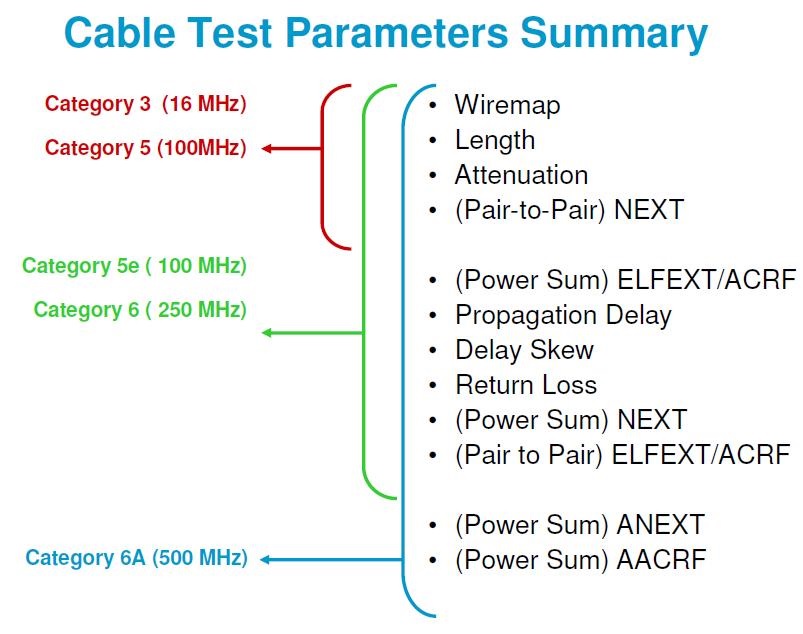
Otro caso muy claro donde el teorema de Shannon hace acto de presencia es en las instalaciones de cableado estructurado, donde una instalación de categoría 3 solo permitirá una velocidad de 10 Mbps mientras que una instalación de categoría 5e permitirá 1000 Mbps, es decir 1 Gbps y una instalación de categoría 6A permitirá 10 Gbps. ¿En que se diferencian estas instalaciones entre sí? Fundamentalmente en el ancho de banda de las señales que dejan pasar sin dificultad, 16 MHz para la categoría 3, 100 MHz para la categoría 5e y 500 MHz para la categoría 6A.

Categorías TIA/EIA de cableado estructurado junto con los parámetros a verificar

Para mas detalles sobre velocidades y anchos de banda en instalaciones de cableado estructurado, se puede consultar la siguiente entrada que está en el blog dedicado a fibra óptica e instalaciones de redes en general y que también llevamos desde el instituto Tartanga: Categorías de cableado estructurado y aplicaciones de las mismas.

Y si bien hasta ahora los ejemplos anteriores han sido referidos a cables de cobre, como se ha dicho al comienzo, el teorema de Shannon es válido para cualquier sistema de transmisión actual o incluso para cualquier nuevo sistema que se descubra en el futuro.

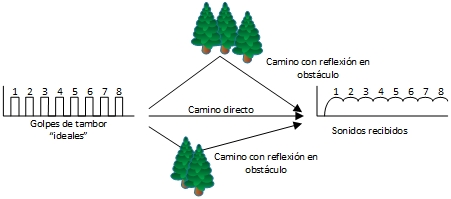
Y aunque no lo conocieran en su momento, también ha afectado a todas las comunicaciones en el pasado, por ejemplo a las comunicaciones mediante tambores: en este caso se ve con claridad que el límite de velocidad vendrá dado por la velocidad con la que el emisor puede golpear el tambor produciendo sonidos lo suficientemente separados para que los pueda identificar el receptor. Suponiendo que el tambor se comporta como una fuente de sonido ideal, el medio, que en este caso es el aire, no se comporta en absoluto con un sistema de transmisión ideal, ya que los pulsos de sonido se transmiten sufriendo un cierto retraso y sufriendo también diversas reflexiones y ecos en las propias capas de aire y en los distintos obstáculos que se encuentran en el camino. Los pulsos de sonido llegan al receptor por varios caminos diferentes y por tanto con diferentes retardos entre sí, por lo que el receptor no percibe los diferentes golpes de tambor separados de forma nítida, sino con una cierta mezcla entre ellos. A medida que aumenta la velocidad de envío de sonidos el efecto de mezcla en el receptor aumenta, llegando un momento en el que no es posible diferenciar los golpes individuales en el tambor y por tanto, no es posible interpretar la información recibida.

Parece claro que si además se está en una situación de mucho ruido ambiente -cerca de una catarata, con ruido de animales, con el ruido producido por una tormenta o con cualquier otra clase de ruido, la relación señal a ruido del canal de comunicación será menor, lo que trae como consecuencia una mayor dificultad al receptor para identificar los sonidos recibidos. Si se quiere mantener la comunicación, el emisor tendrá que aumentar el nivel de señal enviado o disminuir la velocidad de envío de los sonidos. 

Comunicación mediante tambores con buena relación señal a ruido

Comunicación mediante tambores con mala relación señal a ruido

Lo mismo se puede decir respecto a las comunicaciones mediante señales de humo, que todos hemos podido ver en las ya antiguas películas de indios y vaqueros. Este sistema de comunicación también tiene un ancho de banda determinado, que viene dado, entre otras circunstancias, por el tiempo que tardan en disiparse en el aire las nubes de humo producidas por el emisor. Si el transmisor produce nubes de humo “ideales” a mucha velocidad, se producirá un cierto solapamiento en la atmósfera entre nubes de humo consecutivas, llegando un momento en que el receptor tendrá una gran dificultad para observar las nubes individuales producidas. A partir de ese momento, cualquier aumento en la velocidad de producción de nubes de información provocará que el receptor pase a observar prácticamente una única nube suspendida en el aire, haciéndose imposible la transmisión de información. Al igual que en el caso anterior de transmisión de sonido, también en este caso la relación señal a ruido del medio de transmisión influirá en la velocidad máxima a la que se puede enviar información. Ahora el ruido se debe a aquellas condiciones climáticas que dificultan la observación de las nubes de información al receptor, como la presencia de lluvia o niebla. En estos casos, el transmisor deberá de disminuir la velocidad a la que produce las nubes de información para permitir al receptor la identificación de las mismas o, manteniendo la velocidad, deberá de generar nubes de mayor intensidad, pero en este caso, el mayor tiempo que se necesitará para que se disipen en el aire, frenará de nuevo la velocidad de transmisión. De nuevo el teorema de Shannon limitando la velocidad máxima……

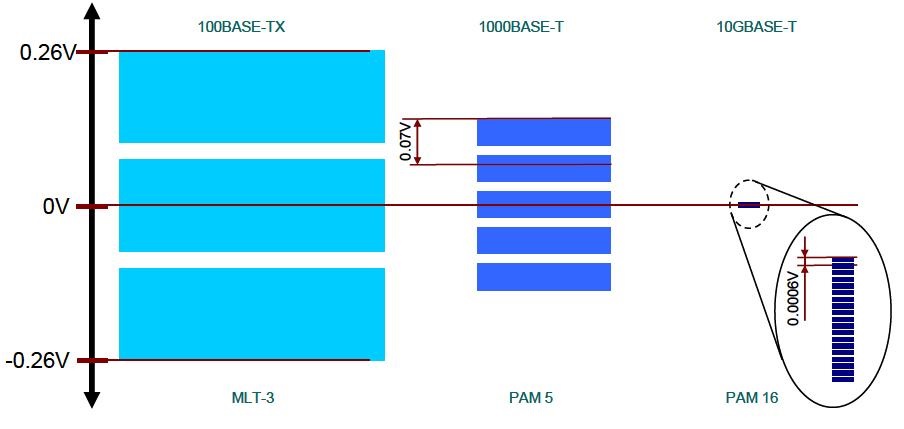
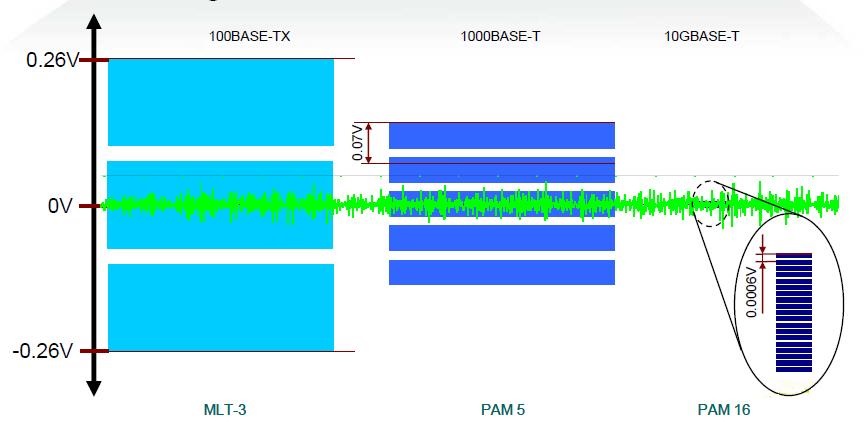
Y aunque es cierto es que los medios de transmisión continuamente están aumentando las velocidades máximas disponibles, la forma en que lo consiguen es o bien mejorando el ancho de banda o bien mejorando la relación señal a ruido, es decir, cumpliendo con lo establecido en el teorema de Shannon. Cuando en un medio de comunicación mejoramos el ancho de banda, por ejemplo al pasar del par de cobre del viejo sistema telefónico analógico a la fibra óptica o los cables coaxiales empleados en las redes FTTH y en HFC, directamente se pueden enviar señales de más bits por segundo, aun empleando el mismo sistema de codificación. En cambio, cuando ya no es posible aumentar el ancho de banda, todavía podemos mejorar la relación señal a ruido, como por ejemplo utilizando cables apantallados o trenzando los pares para evitar la influencia entre ellos. Con este sistema podemos utilizar codificaciones multinivel más complejas de tal manera que aunque la señal transmitida no aumenta los cambios en la línea por segundo (baudios), si que se aumentan los bits por segundo transmitidos. En la siguiente imagen se observan las codificaciones MLT-3, PAM 5 y PAM 16 utilizadas respectivamente en los sistemas Ethernet 100 BASE-TX, 1000 BASE-T y 10GBASE-T

Evidentemente, cuantos mas niveles de señal se puedan transmitir, mas bits se podrán codificar en cada cambio de la señal. Así, con el sistema PAM16 se pueden transmitir hasta 4 bits en cada cambio de la señal (2^4=16). Por supuesto, para que todo esto pueda funcionar es necesario que el nivel de ruido en cada uno de los pares del cable del sistema 10GBASE-T debe de ser muy inferior al ruido que puede haber en los pares de un cable que se utiliza para transmitir señales de 100-BASE-TX o 1000-BASE-T, ya que de otra forma la señal PAM16 quedaría absolutamente enmascarada por el ruido y sería imposible la comunicación.

Para mas información sobre la importancia del ruido en los sistemas de cableado estructurado se puede consultar la siguiente entrada del blog:  Por qué es tan importante no sobrepasar los 100 metros en las instalaciones de cableado estructurado.