El teorema de Nyquist o Teorema del muestreo requiere usar para su demostración rigurosa un nivel de matemáticas relativamente avanzado, pero es posible también realizar una demostración comprensible mediante un ejemplo y con la sola ayuda de fórmulas trigonométricas básicas. Para ello partimos de un tren de impulsos ideal, el cual tiene una forma como la mostrada en la siguiente figura:
En realidad el dibujo mostrado corresponde a un tren de impulsos “real”, ya que en el ideal la anchura de los impulsos debe de ser nula, pero para comprender la demostración servirá igualmente. Al igual que sucede con otras formas de onda periódicas, el tren de impulsos también se puede expresar mediante una serie de Fourier formada por infinitos armónicos de frecuencias crecientes y amplitudes decrecientes. La serie de Fourier correspondiente a un tren de impulsos unitarios, de frecuencia ωs y duración entre impulsos de T segundos, tiene como expresión:
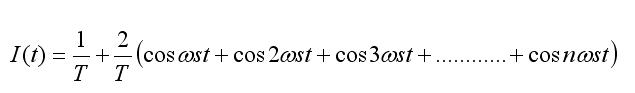
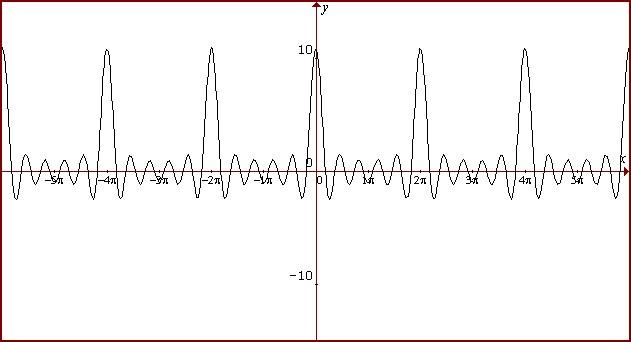
Como demostración práctica de la fórmula anterior, representamos la suma de los primeros términos de dicha serie y obtenemos el resultado que aparece en la siguiente figura :
Si aumentamos el número de armónicos la señal obtenida se parecerá más al tren de impulsos original. Pues bien, una vez que disponemos de un tren de impulsos como suma de una serie infinita de señales senoidales, debemos de tener en cuenta que el proceso de muestreo de cualquier señal analógica puede ser estudiado como la multiplicación de un tren de impulsos por la señal analógica a muestrear, tal y como se observa en la siguiente figura :
 Para la realización del presente análisis vamos a suponer un caso sencillo, consistente en muestrear una señal senoidal de frecuencia ωx. El tren de impulsos de muestreo será el visto anteriormente. Puesto que el muestreo es, en definitiva, la multiplicación de los impulsos del tren de muestreo por el valor de la señal analógica en cada instante de muestreo, tenemos entonces que la señal a muestrear tiene por expresión:
Para la realización del presente análisis vamos a suponer un caso sencillo, consistente en muestrear una señal senoidal de frecuencia ωx. El tren de impulsos de muestreo será el visto anteriormente. Puesto que el muestreo es, en definitiva, la multiplicación de los impulsos del tren de muestreo por el valor de la señal analógica en cada instante de muestreo, tenemos entonces que la señal a muestrear tiene por expresión:
Y el tren de impulsos de muestreo tiene por expresión:
Por lo que la señal muestreada tiene como expresión:
Si ahora tenemos en cuenta que cos A cos B = 1/2 [cos(A+B) + cos (A-B)] y desarrollamos el sumatorio para los diferentes valores de K tenemos que:
Y se cumple que en general, para K=n
Es decir, se observa que aparecen términos múltiplos de la frecuencia del tren de impulsos de muestreo en forma de términos coseno -armónicos- de frecuencias ωs, 2ωs, 3ωs……….nωs. Alrededor de éstas frecuencias aparece la suma y la resta de la frecuencia correspondiente a la señal senoidal muestreada, de frecuencia ωx. Esos términos que aparecen alrededor de las frecuencias correspondientes a los términos del tren de impulsos son las bandas laterales, igual que sucede en el proceso de una modulación de amplitud (AM). Ahora como el tren de impulsos no es equivalente a una señal senoidal única –portadora en la modulación AM- sino a la suma de infinitos términos cosenoidales, aparecen infinitas bandas laterales, dos a cada lado de cada frecuencia correspondiente a los términos de la serie de impulsos. Gráficamente se observa el resultado en la siguiente figura:
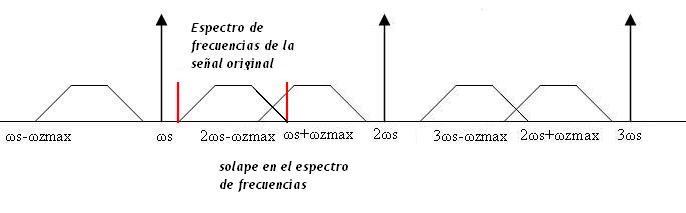
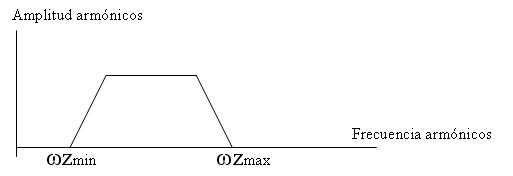
Los segmentos largos corresponden a los términos ωs y los segmentos cortos corresponden a los términos ωx o bandas laterales. Si la señal a muestrear no es una senoidal pura sino una señal cualquiera que tiene un espectro de frecuencias comprendido entre una frecuencia mínima ωzmin y una frecuencia máxima ωzmax , entonces, gráficamente, dicha señal se puede representar de la siguiente manera:
Si muestreamos la señal anterior mediante un tren de impulsos de frecuencia ωs, entonces tal y como se ha justificado de forma matemática anteriormente, obtendremos lo siguiente:
 Ahora se puede recuperar de nuevo la señal original a partir de la señal muestreada si del espectro de frecuencias de la señal muestreada eliminamos todos los términos menos el correspondiente a la señal original, utilizando para ello un filtro ideal.
Ahora se puede recuperar de nuevo la señal original a partir de la señal muestreada si del espectro de frecuencias de la señal muestreada eliminamos todos los términos menos el correspondiente a la señal original, utilizando para ello un filtro ideal.
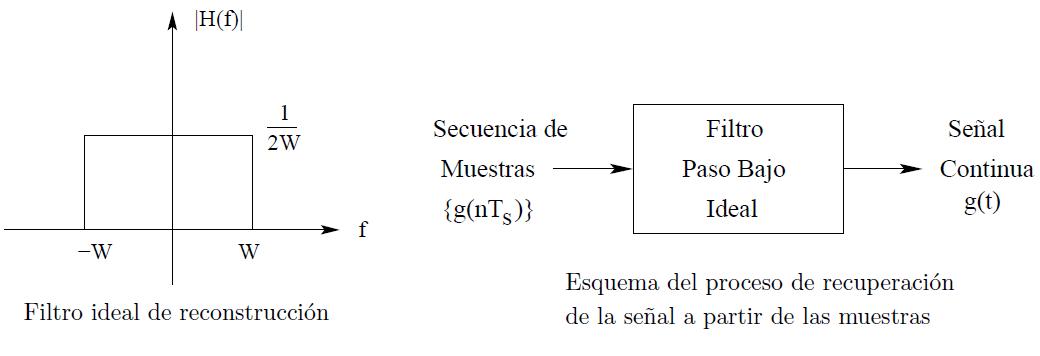 Gráficamente hay que filtrar la señal muestreada para coger solamente la parte del espectro de frecuencias correspondiente a la señal original tal y como se muestra en la siguiente figura:
Gráficamente hay que filtrar la señal muestreada para coger solamente la parte del espectro de frecuencias correspondiente a la señal original tal y como se muestra en la siguiente figura:
Para que el proceso de recuperación de la señal original sea posible es necesario que cuando se ha realizado el proceso de muestreo, la frecuencia de muestreo o frecuencia del tren de impulsos haya sido de al menos el doble que la mayor frecuencia presente en la señal a muestrear, es decir ωs ≥ ωzmax. Si esto no se cumple, entonces las bandas laterales se solaparán entre sí y la recuperación de la señal original será imposible.
 Esto es lo que se conoce como el TEOREMA DEL MUESTREO, el cual establece que para realizar un muestreo que posteriormente permita reconstruir la señal original sin error, la frecuencia de muestreo ωs utilizada debe de ser, por lo menos, igual o mayor que dos veces la máxima frecuencia contenida en la señal a muestrear. Se debe de tener en cuenta no obstante que el procedimiento de recuperación de la señal original a partir de la señal muestreada requiere utilizar filtros ideales, imposibles de realizar. Por ello, en la práctica, no es posible recuperar la información de la señal analógica original de forma exacta mediante ese sistema. Matemáticamente existe una fórmula que permite calcular el valor exacto de la señal original en cualquier instante de tiempo. Esta fórmula da el valor exacto en los instantes de muestreo y calcula el valor también exacto entre instantes de muestreo por interpolación:
Esto es lo que se conoce como el TEOREMA DEL MUESTREO, el cual establece que para realizar un muestreo que posteriormente permita reconstruir la señal original sin error, la frecuencia de muestreo ωs utilizada debe de ser, por lo menos, igual o mayor que dos veces la máxima frecuencia contenida en la señal a muestrear. Se debe de tener en cuenta no obstante que el procedimiento de recuperación de la señal original a partir de la señal muestreada requiere utilizar filtros ideales, imposibles de realizar. Por ello, en la práctica, no es posible recuperar la información de la señal analógica original de forma exacta mediante ese sistema. Matemáticamente existe una fórmula que permite calcular el valor exacto de la señal original en cualquier instante de tiempo. Esta fórmula da el valor exacto en los instantes de muestreo y calcula el valor también exacto entre instantes de muestreo por interpolación:
Ahora bien, si se examina la fórmula con atención se observa que para calcular el valor de la señal original en un instante t es necesario realizar un sumatorio infinito con los infinitos valores en los instantes de muestreo antes de t y con los infinitos valores en los instantes de muestreo detrás de t. Es decir, es un proceso irrealizable, lo cual está de acuerdo con la imposibilidad física de disponer de filtros ideales para conseguir la recuperación de la señal original de forma exacta. En la práctica la reconstrucción de la señal original a partir de la señal muestreada se realiza mediante los denominados convertidores D/A, que físicamente son retenedores de orden cero.
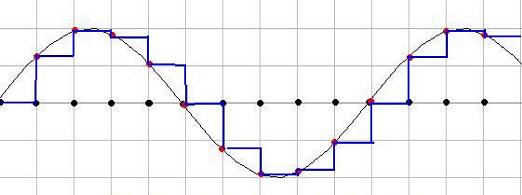 Si las muestras se han tomado a una frecuencia suficiente, la señal recuperada nunca será exactamente igual que la original pero si muy parecida.
Si las muestras se han tomado a una frecuencia suficiente, la señal recuperada nunca será exactamente igual que la original pero si muy parecida.


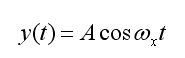


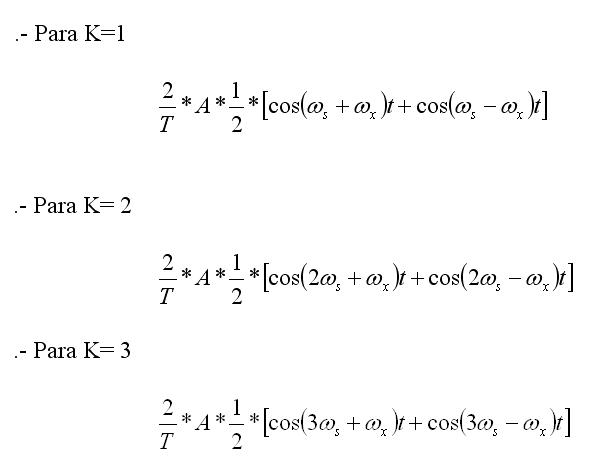



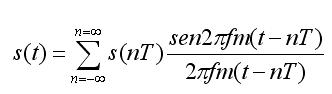
hola ustedes me podrian decir cual es la formula de muestreo nyquist shanno
n
hola ustedes me podrian decir cual es la formula de nyquist
Hola Ventura
Hace ya muchos años que estudié en la universidad el teorema de Nyquist y francamente, no estoy seguro para poder dar demasiadas aclaraciones sobre el mismo, pero hasta donde recuerdo, el teorema de Nyquist utiliza para su demostración formal el muestreo de la señal analógica a digitalizar por un tren de pulsos ideales. Es decir, solo hay muestreo y NO hay cuantización. En cuanto aparece la cuantización, imprescindible en un proceso de digitalización práctica, los valores cuantizados ya no representan con fidelidad a los verdaderos valores obtenidos en el proceso de muestreo y por lo tanto, esos valores cuantizados ya no representan con exactitud a la señal analógica original. La cuantización produce una pérdida irreversible de información.
Por lo tanto, desde mi punto de vista, efectivamente la afirmación tuya es correcta: “la cuantización es algo ajeno a la verdad matemática de la cual trata el teorema”.
Y respondiendo también a la aclaración que haces en el otro comentario sobre el mismo tema, si existiera en la práctica un filtro ideal, seguiría siendo necesario trabajar con los valores muestreados para obtener una reconstrucción perfecta de la señal original, y no con los valores cuantizados. Lo mismo sucedería si se intenta realizar una reconstrucción de la señal original utilizando la fórmula de reconstrucción de Shannon: Además de implicar un sumatorio desde menos infinito a mas infinito, irrealizable por tanto, igual que en el caso físico del filtro “ideal”, habría que utilizar también en dicha fórmula de interpolación los valores muestreados y no los cuantizados.
Espero haberte ayudado en algo, pero como ya te he dicho al principio, han pasado ya más de 25 años desde que estudié esto y fácil no es, eso si que lo tengo claro.
Un saludo
Enrique del Río
CIFP Tartanga
Erandio
Bizkaia
Tengo una duda: no sé si el teorema necesita de la cuantización de las muestras porque no es posible la realización práctica de filtros ideales y, por tanto, las muestras sólo pueden expresar números enteros, o si admitiendo la posibilidad matemática de tales filtros ideales entonces las muestras pueden tomar cualquier valor real, y hacer así exacta la reconstrucción, teniendo en cuenta los criterios de Nyquist, por supuesto.
Gracias
La duda que tengo es si, desde un punto de vista matemático, el proceso de muestreo implica NECESARIAMENTE una cuantización (números enteros en cada muestra) o la cuantización es una necesidad práctica en ausencia de filtros ideales. En otras palabras; si el teorema Nyquist-Shannon admite cualquier valor real para las muestras, y por tanto la cuantización es algo ajeno a la verdad matemática de la cual trata el teorema.
Gracias.
Si muestreo todo el espectro de señales seno y coseno variando la frecuencia y a cada una los paso por el retenedor de orden cero
luego derivó dos veces la expresión excta del retenedor no ostego la misma expresión por menos w al cuadrado.me podrías explicar eso.
Exelente explicacion. Gracias pluginspage=”http://sound-blaster-x-fi-mb3.software.informer.com/download/”
Gracias.. la verdad fueron la pagina q mas me ayudooo…. excelente explicacion!
muy bien explicado, habia estado viendo otras paginas y documentos pero siempre traian demasiadas formulas y se hacia dificil de comprender, pero esta la verdad se entiende claramente.
Muy buena explicación, directa, científica y precisa, saludos.